In the paper “DomLock: a new multi-granularity locking technique for hierarchies” the authors present an interesting technique for locking objects that follow a hierarchical structure. Several applications that operate on objects that form a hierarchy suffer from synchronization bottlenecks because of lock contention. When several transactions operate on different parts of the data hierarchy, there is contention which restricts concurrency.

Background

Data hierarchies are practical when designing systems because they model the data in an organic, human understandable structure. A hierarchy has a containment relationship between objects where one object is said to contained in another or in other words, a child. This definition, extends to structures like trees, cycles, graphs, lists etc.

Locking and Hierarchies

The problem with hierarchies is that they do not allow trivial multi-writer access to the component objects. When we consider locking as a primitive to allow safe concurrent access to the structure, we need to reason about the granularity of locking. Coarse grained locking restricts concurrency but promotes safety and vice a versa. This is one of the reasons why application programmers resort to this way of locking the structures. Fine-grained locking is better for concurrency, but it needs carefully designed primitives controlling the access to maintain invariants on the data.

Multi-Granularity Locking

Multi-granularity locking or MGL locks the entire hierarchy or a subset of it to prevent fine locks and allows concurrent access to non overlapping parts of the hierarchy. The problem with MGL is that the traversal cost to find overlaps and lock structures is high. MGL can be achieved by intention locks but intention locks lock the path to the required subtree from the root which makes them well suited for large data structures.

DomLock: Dominator Based Locking

Dominators

For any graph, a node d is a Dominator of node n if all the paths from the root to node n pass through d.

A dominator d is an Immediate Dominator of node n if there exists no other dominator on the paths between d and n.

This gives us a few trivial relationships in specific data structures.

• For trees, each node’s parent is its immediate dominator.
• In trees, for a set of nodes, their lowest common ancestor is the dominator.
• In a DAG, nodes that belong to all the reference paths become the dominators.
• When there are cycles, there can be infinite dominators. In such a case, the node of entry to the cycle is considered the dominator of the nodes in the cycle.

Locking with Dominators

Locking the dominator of a set of nodes is enough to lock the nodes. This leads to an observation that the closer the nodes intended to be locked and their dominator is, the higher the concurrency. To maximise concurrency, thus, the immediate dominator is chosen as the lock node.

Per-Thread Locking algorithm

function run(){
    S = GenerateRequests();
    LockAll(S)
        // Critical Section
    UnlockAll(S);
} 

function LockAll(S){
    dom = FindDominator(S);
    if(pool.IsOverlap(dom) == false)
        pool.insert(dom);
    else{
        // retry checking;
    } 
        
}

function UnlockAll(S){
    dom = FindDominator(S);
    pool.remove(dom);
}

Logical Intervals

When running the locking algorithm it is necessary to maintain that the overlapping substructures in the hierarchy are not locked at the same time. This overlap can be found by traversing the structure which is vastly expensive for every lock request issued for a large hierarchy. As an alternate, DomLock uses logical intervals to efficiently check the overlap.

For a graph $G = (E, V )$, where $V$ is the set of vertices on the graph and $ E \subseteq V \times V $ is the set of directed edges between the vertices, we define a function $ \mathcal{L} : V \rightarrow \mathbb{N} \times \mathbb{N}$, such that for any element $ v \in V, \mathcal{L}$ is a pair $[x,y]$ with $ x \leq y $, that denotes the logical interval associated with $v$

Property 1 (Subsumption):

For each element $v \in V $, the logical interval $ \mathcal{L(v)}$ subsumes $ \mathcal{L(v’)}$ for all descendants $v’$ reachable from $v$. Thus, if $ \mathcal{L(v)} = [x, y]$ and $ \mathcal{L(v’)} = [x’, y’]$, then $x \le x’ $ and $ y \ge y’$

ModifiedDFS for Computing Logical Intervals

count = 0;

function ModifiedDFS(node) {
    if(node == null)
        return
    if(node.explored == false){
        if(node.isLeaf || node.isActive){
            count++;
            node.interval.low = count;
            node.interval.high = count;
        }
        else {
            node.isActive = true;
            for( child in node.Children) {
                ModifiedDFS(child)
            }
        }
        node.explored = true;
        node.active = false;
    }
    for(parent in node.Parents){
        UpdateParent(parent, node)
    }
    
    node.parentUpdated = true;
}

UpdateParent to Update Intervals of the Parent nodes

function UpdateParent(parent, node){
    if(parent == null){
        return true;
    }
    if(parent.interval == defaultInterval){
        parent.interval = node.interval
    }
    else{
        if(parent.interval.low > node.interval.low){
            parent.interval.low = node.interval.low;
        }
        if(parent.interval.high < node.interval.high){
            parent.interval.high = node.interval.high;
        }
    }
    if(parent.parentUpdated){
        for(w in node.Parents){
            UpdateParent(w, parent)
        }
    }
}

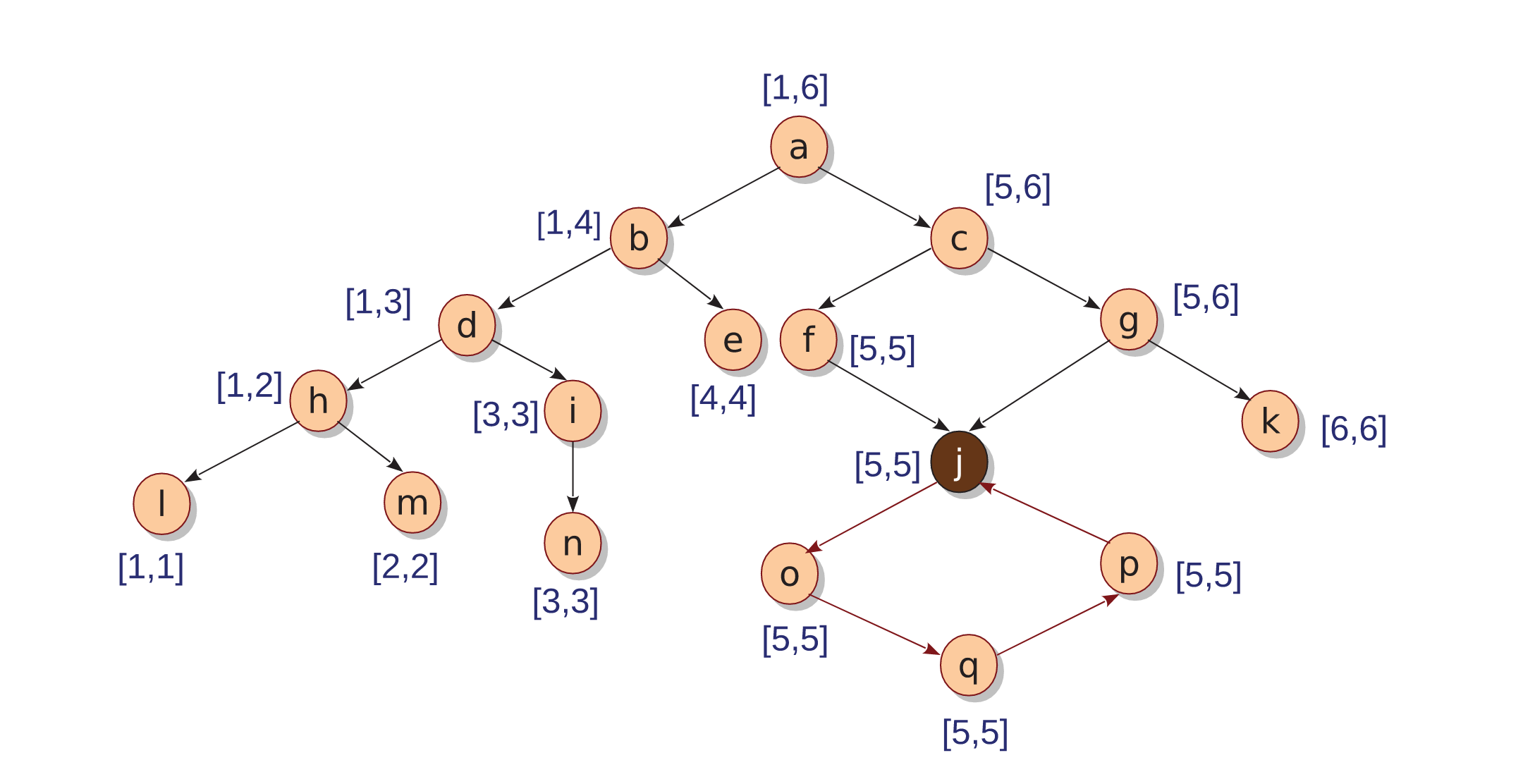Graph with the Node Intervals assigned using the above algorithms

Locking a Sub-Hierarchy with DomLock

Finding a Dominator

When we wish to lock a specific set of nodes, we find the immediate dominator of the nodes of that set. This process involves traversing the graph from the root until a node is found with a suitable interval. If none of the nodes dominates the set of nodes to be locked, the root is returned as a default. The algorithm findDominator() is called on the root node of the graph.

function findDominator(node, S) {
    setLow = minimum(S.nodes.low);
    setHigh = maximum(S.nodes.high);
    ptr = node
    for(x in properDescendents(node)){
        if(x.low <= setLow && x.high >= setHigh){
            ptr = x;
            break;
        }
    }
    if(ptr.interval != node.interval){
        return findDominator(ptr, S)
    }
    else {
        return node;
    }
}

What happens if there is an overlap?

It is bound to happen that when a transaction wishes to lock a set of nodes, there is a conflict. This conflict will be detected when we go to acquire the locks on the dominator. If the dominator for two sets is not the same, the lock should not be granted. To check if there is a conflict between threads, DomLock maintains a pool of threads with the intervals of their locks. Since the intervals are number types, they can be easily hashed and searched. When we wish to acquire a lock for an interval which overlaps with the currently held locks. If no overlap is found, then the thread is trying to acquire a lock for nodes which are not currently locked by another thread and the lock can be granted. This lookup is followed by adding the new thread entry to the pool indicating an acquired lock.

To prevent race conditions and invariants, the lookup and update of the concurrent pool should be atomic. A simple solution is to use Reader-Writer locks. The lookup requires a reader-lock which allows concurrent lookups and the update requires a writer-lock which is mutually exclusive. This also means that the update operation needs to ensure that there were no concurrent modifications between when the read and write locks were acquired.